Z3 SMT Solver
By Hongjia Wu, Bohao Zhang, Yujing Gong, Qiaoqiao Li
Delft University of Technology
Abstract
Z3 is a high-performance theorem prover developed by Microsoft Research. Z3 is used for program analysis, testing, and verification. Basic implementation can be carried out through its online tool using SMT 2.0. Complicated formulation could be implemented through programming in local Z3 version. The goal of this chapter is to analyze Z3's software architecture and help users take advantage of the product. In this chapter, we will introduce Z3 with respect to stakeholders, context view, development view, variability perspective, evolution perspective, deployment view, and usability view analysis.
Table of Contents
| # | Title |
|---|---|
| 1 | Introduction |
| 2 | Stakeholder Analysis |
| 3 | Context View |
| 4 | Architecture |
| 5 | Development View |
| 6 | Variability Perspective |
| 7 | Evolution Perspective |
| 8 | Deployment View |
| 9 | Usability View |
| 10 | Conclusion |
Introduction
Z3 is a Satisfiability Modulo Theories (SMT) problem solver developed by the Microsoft Research organization. SMT problem derives from Satisfiability (SAT) problem. SAT determines if there exists an interpretation that satisfies a given Boolean formula in computer science field. In other words, it determines whether a given Boolean formula is TRUE or FALSE. If a Boolean formula is TRUE, SAT solver returns "satisfiable", otherwise, it returns "unsatisfiable". For example, the formula a AND NOT b is satisfiable because one can find the values a = TRUE and b = FALSE, which make (a AND NOT b) = TRUE. In contrast, a AND NOT a is unsatisfiable since one cannot find a value a that makes (a AND NOT a) = TRUE. SAT is limited to Boolean formulas while SMT extends this kind of decision problem to cover other logical formulas. SMT contains combinations of background theories expressed in classical first-order logic. Examples of background theories that commonly occur in computer science are the theories of various data structures such as real numbers, lists, arrays, bit vectors and so on [1].
Since determining whether a logical formula is satisfiable or not is quite fundamental but can also be quite complex in computer science field, Microsoft has developed Z3 as a tool to solve these kind of problems in many large projects [2]. Its major applications are verifying device driver, proving the correctness of programs, testing software, and so on. Z3 can be employed in industry and academia. It is one of the best SMT solvers among all mainstream SMT solvers and has already gained four champions in global SMT solvers competition [3].
The core theory solver of Z3 is based on the congruence closure algorithm. And the congruence closure takes the satellite theories (bit-vectors, arithmetic, arrays, partial orders, tuples) as its peripheral solvers. Architecture of Z3 will show these components. The source code of Z3 is written in C++. However, it also provides a sequence of programmatic APIs including JAVA, .NET, C, OCaml, and Python.
Stakeholder Analysis
Many individuals and groups are involved in the development of Z3. They are called stakeholders . Stakeholders are identified according to their interests, concerns, and impacts on Z3.
Owner/Acquirer/Funder
- Microsoft
It is the need of Microsoft's internal customers that drives the development and research of Z3. Microsoft owns Z3 and it has been supporting the development of Z3 since the beginning of this product. Microsoft is regarded as the owner, the acquirer, as well as the funder of this product.
Researchers/Developers/Maintainers/Communicators
Z3 was used internally at the beginning. The official Microsoft Research website shows that these listed three people are major researchers and developers of Z3. After Z3 was moved to GitHub in 2015, they have been actively participating in its further development and improvement by making contributions and making decisions of the contributions from the open source community. They function as maintainers to manage Z3's evolution. Also, they act as communicators to teach Z3 at summer schools and provide slides and tutorials online.
Testers
- Nikolaj Bjorner
- Leonardo de Moura
- Christoph M. Wintersteiger
- Some individual users
Z3 has a z3test repository that shows Nikolaj Bjorner, Leonardo de Moura, and Christoph M. Wintersteiger are also testers of Z3. They sometimes ask users are to help test Z3. This Facebook post gives us an example of this kind of request. Besides, other users are also welcomed to add tests and benchmarks to z3test repository.
Community Contributor
Dan Liew is actively participating in the development of Z3 on GitHub. He makes his own contributions and sometimes offers help to the develop team. However, Dan is not a member of Microsoft but an active user on GitHub. So we consider him as a community contributor.
Users
Z3 is used in many program analysis, testing, and verification tools of Microsoft Research. Additionally, Z3 provides free use of the resource for any academic research group or individual. Its users can be classified into the following categories:
Microsoft program verification projects, e.g., Boogie,VCC, Dafny, Chalice, Spec#, and Fstar
Microsoft program testing and analysis projects, e.g., Pex, Yogi, and Vigilante
Other Microsoft applications, e.g., bounded model-checking of model programs, termination, security protocols, business application modeling, cryptography, and model-based testing (SQL-Server)
Academic research groups and individuals. These entities have free access to Z3. Some users are experienced with coding and could make contributions to the development of Z3. They, in this case, change their roles to developers or testers as mentioned earlier. Therefore, the relationship between developers, testers, and users can be briefly depicted using Figure 1.
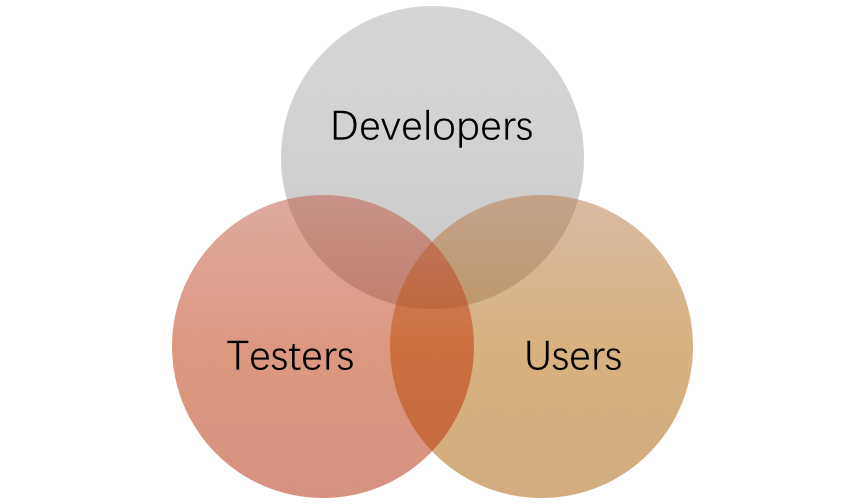
Figure 1. Relationship of developers, testers, and users
Competitors
- Other SMT solvers
Apart from Z3, other mainstream SMT solvers include Ario, CVC3, MathSAT, Simplify, TSAT, Verifun, and Yices. They all have advantages and disadvantages with respect to platform compatibility and feature variability. Users choose one from all SMT solvers that perform most efficiently according to their needs. Therefore, these solvers are considered as the competitors of Z3.
Integrators
Integrators play an important role in the development of a software [4]. Based on the analysis of the above stakeholders, together with the analysis of issues and pull requests on GitHub, integrators of Z3 can be identified as the following people.
These two people are developers and testers of the product. They deal with most of the issues and all the pull requests by making a decision of which ones to merge and which ones to close.
When processing contributions from other developers and users, size, complexity, types of the changes, together with many other factors, will affect how integrators deal with the contributions. Their decision strategies can be classified as fast decision, verification before decision, and help wanted.
Most of the contributions (pull requests) from users are minor mistake corrections like typo corrections and small bug fixes. These kinds of pull requests cost little time of the integrators to deal with and they are often ended with a simple grateful comment from integrators. When dealing with these contributions, integrators only need to consider whether the change is correct and necessary.
When dealing with contributions concerning larger change/improvement of the product, integrators will firstly get a general idea of the changes/improvement and make the first decision of whether the change is necessary or not. If it is an unnecessary change, integrators will express the gratitude and close the pull request. However, if it seems like a necessary and helpful improvement, integrators will have to test the result and verify the improvement. In the testing and verification process, if some additional changes need to make upon the proposed contribution, integrators will commit to the pull request and let the new changes be tested and verified by other users.
When a pull request shows some potential improvements of the product, integrators will decide whether they will do the job themselves or it is more likely to deliver the job to other persons. When they decide to let someone else finish the job, they need to make sure the person they choose is responsible and dedicated.
Power/Interest Grid
Stakeholders have different level of power and interest to a software product. According to the stakeholder analysis, Power/Interest analysis of stakeholders is generated and the corresponding plot diagram is shown in Figure 2. The low-power, low-interest group monitors the trend of the project with minimum effort; the low-power, high-interest group keeps informed closely because Z3 is associated with their self-benefit; the high-power, low-interest group should always be kept satisfied without much effort; the high-power, high-interest group is always dedicating to Z3 and have absolute power of decision-making.
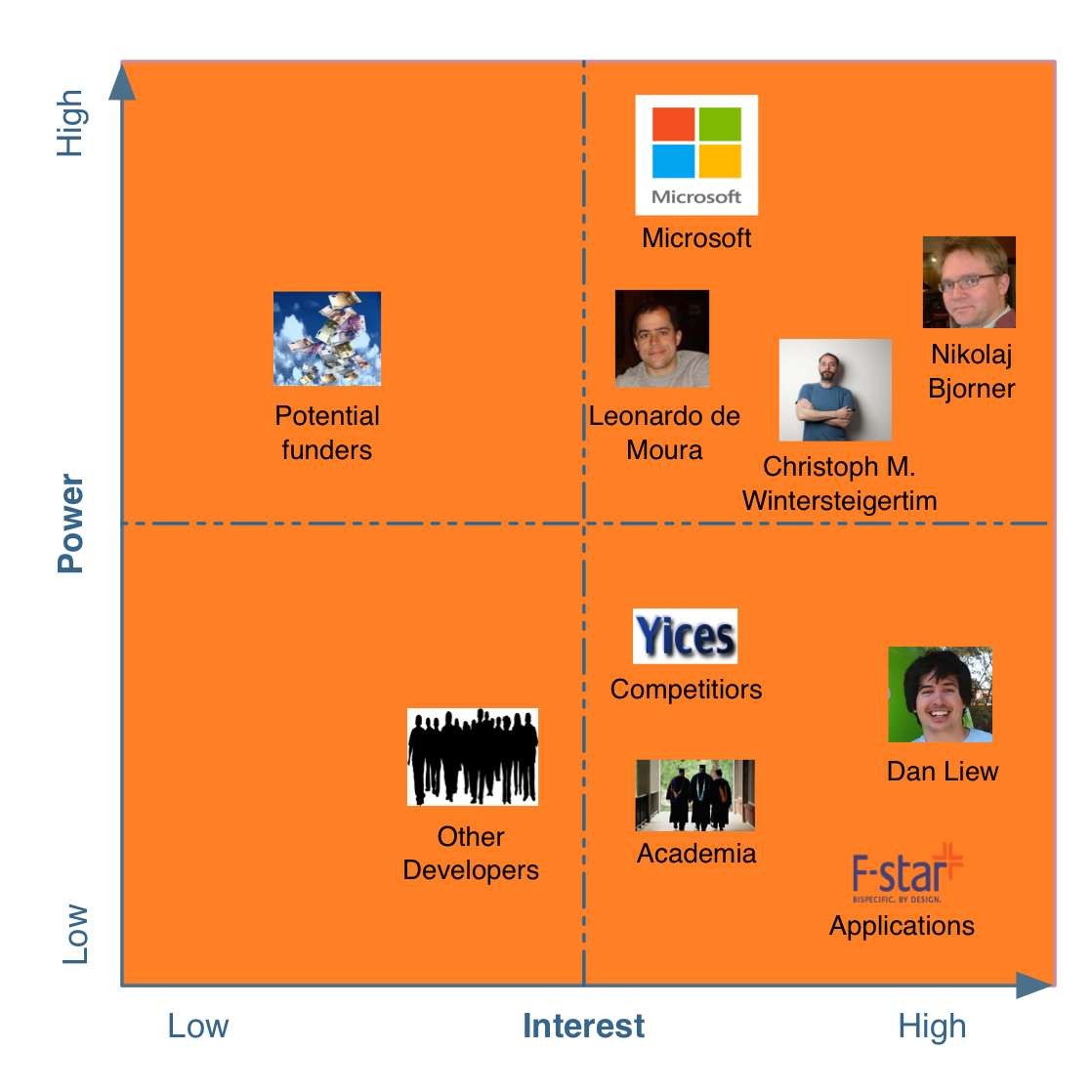
Figure 2. Power/Interest grid
Context View
Based on the analysis of stakeholders, the context view of Z3 is generated to show relationships, dependencies and interactions between the system and its environment. The context diagram (see Figure 3) explains the environment in which the system is operating and the external entities it interacts with.
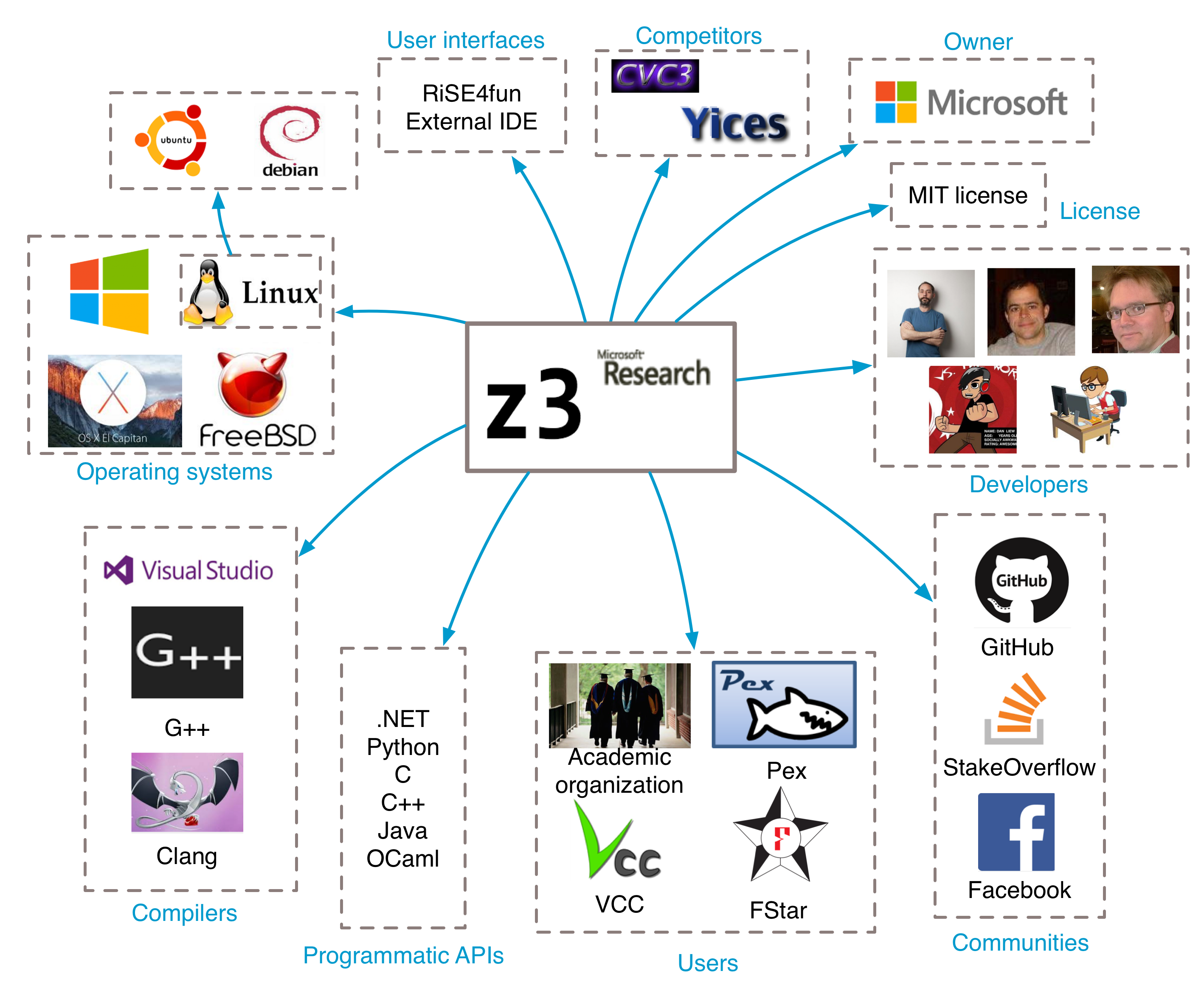
Figure 3. Context view
Figure 3 shows that Z3 runs smoothly on various operation systems including Windows, MacOS X, Ubuntu, Debian, and FreeBSD. Z3 can be built by Visual Studio on Windows or Makefile on other platforms . While the source code of Z3 is written in C++, users can choose from many user interface languages supported by Z3, such as Python, .NET, C, C++, JAVA, and Ocaml.
As a software with many stakeholders, Z3 communicates a lot with external entities. Z3 has a Facebook page, which is used to inform those who are interested in Z3 with its recent situations. Besides, StackOverflow is used to document relevant footprints and offer help to users. Z3, most importantly, makes fully use of GitHub for its further development and improvement. GitHub is used not only as the code repository, but also to offer tutorials, papers, FAQs, and other related information in a completely open way. On the other hand, with the help of GitHub, developers can get inspiration in several areas such as bug fix, code improvement, and new features.
Architecture
Before digging deeping to the architecture details of Z3, let's first take a look at the architecture overview of Z3 [5] to understand how it performs. Z3 integrates an SAT-solver, a core theory solver (Congruence Closure Core), 4 satellite solvers, and an E-matching abstract machine. It's architecture is shown in Figure 4.
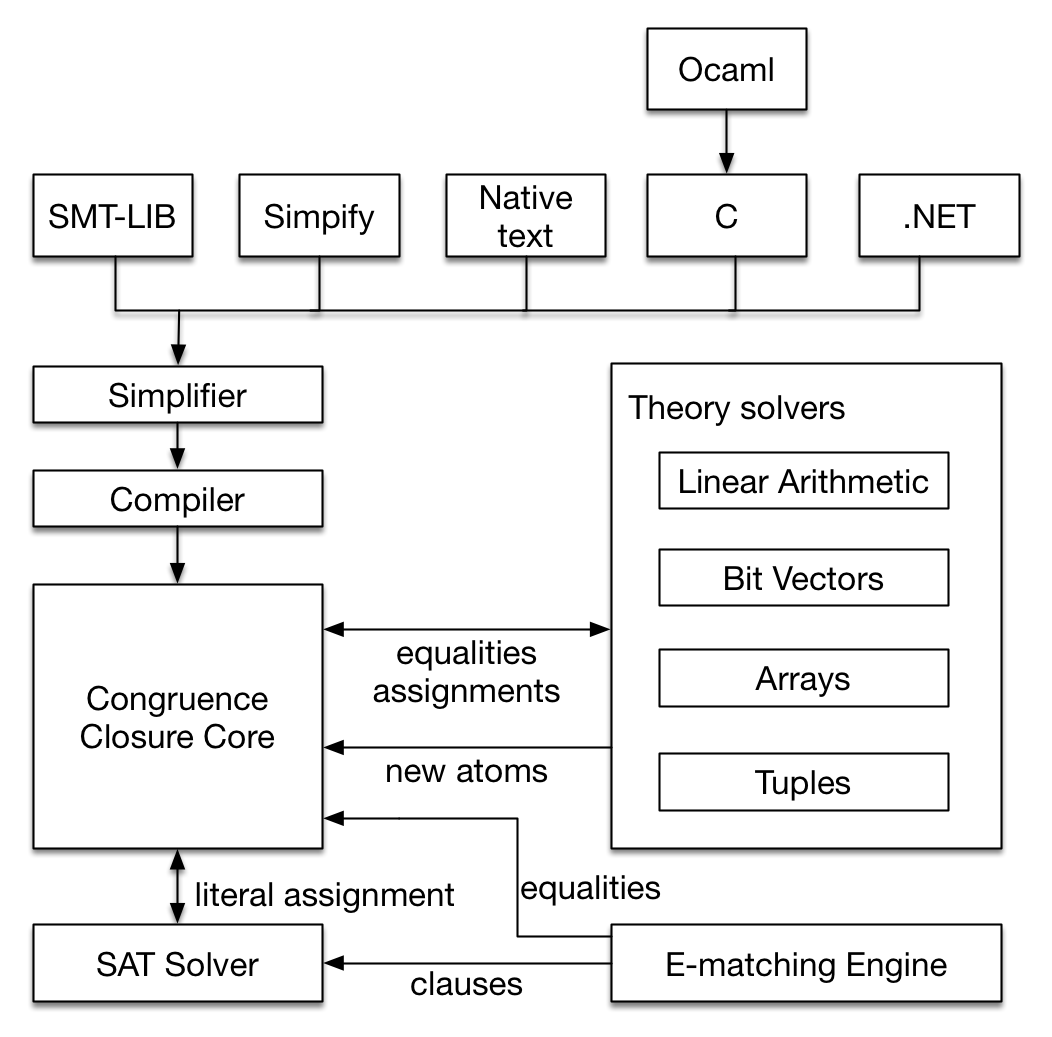
Figure 4. Architecture of Z3
Z3's simplifier applies an incomplete but efficient simplification scheme. For example, it simplifies p^true as p and x=4^f(x) as f(4) (the operator ^ is used as logical AND in these two examples). The compiler of Z3 is considered as a node that converts the simplified input into a different data structure comprising a set of clauses and congruence closure nodes. The Congruence closure core handles equalities and uninterpreted functions. It receives the assignment from the SAT solver and have it processed using a method called E-matching. SAT solver solves the formula and passes the result back to Congruence Closure Core. Congruence Closure Core then processes the result. There are 4 major types of Theory Solvers that are used for arithmetic, arrays and others. They are Linear arithmetic, Bit vectors, Arrays, and Tuples. The theory solvers are based on the congruence closure algorithm, which is the algorithm used by most SMT solvers. Thus, congruence-closure can be considered as a core solver and other theory solvers as peripheral solvers.
Development View
After having a general idea of the architecture of Z3, we can now analyze code organization, code quality, module and layer dependencies, and test infrastructure of Z3 to form the development view.
Code Organization
Z3 was not an open source software in the first place but was used inside the company and research team. Thus, the source code of Z3, at first, was not well-organized [6]. After Z3 became available to all people, the developers started to rewrite some parts of the code to offer better use to other users and cleaned up the Z3 repository. They have put all code into the z3/src directory and made it easier to find a certain module in the sub-directories of z3/src. Now the source code of Z3 is much more readable and well-organized.
Repository of the Z3 project has the following four sub-directories:
z3/doc, which is used to generate API doc files and code doc files.z3/examples, which provides a bunch of examples or benchmarks that help users to understand how to formulate a problem in different API languages.z3/scripts, which contains files for updating external Z3 API.z3/src, which contains all core modules of Z3.
Organization of source code is shown in Figure 5. The organization is clear and understandable.
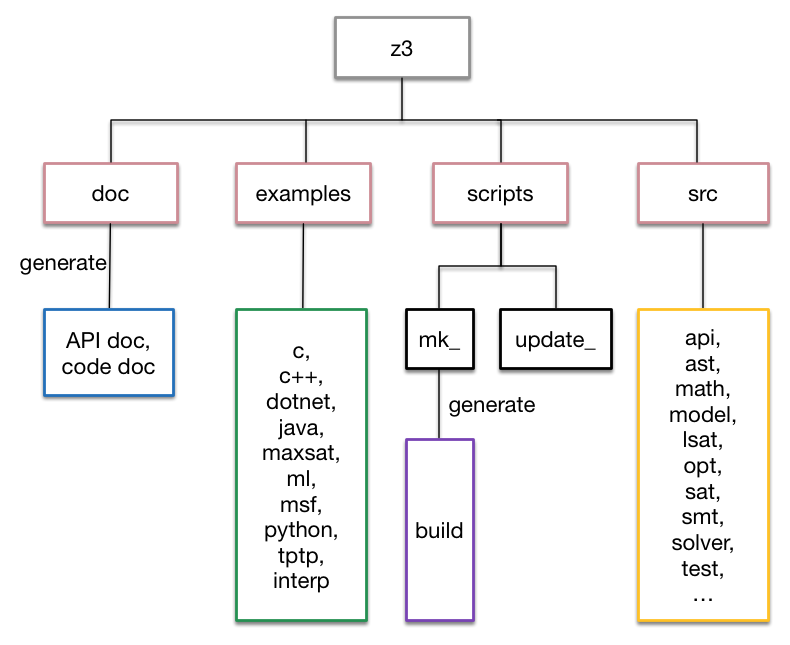
Figure 5. Code organization
Code Quality Evaluation
Having studied the source code of Z3, we now evaluate its code quality using iPlasma 6.1. As an example, we analyze a Java API source code of Z3. The analysis result is shown in Figure 6.
Figure 6. iPlasma pyramid of Java source code
The meanings of metrics in Figure 6 are illustrated in Table 1.
| Metrics | Description |
|---|---|
| NDD | Number of directly derived sub-class |
| HIT | Height of inheritance trees |
| NOP | Number of packages |
| NOC | Number of classes |
| NOM | Number of methods |
| LOC | Lines of code |
| CYCLO | Cyclomatic complexity |
| CALL | Number of each method calls |
| FOUT | Scattered calls |
Table 1. Meaning of metrics in iPlasma
It can be observed from Figure 6 that inheritance trees tend to have many depth levels and base classes with a large number of directly derived sub-classes. And the classes tend to be defined in many methods and organized with a larger number per package. The methods are rather short yet having complex logics. Besides, the high coupling density also derives from low coupling dispersion. These phenomena testify that developers are trying their best to avoid technical debts in Z3. Nevertheless, since Z3 is a large, complicated and NPC based mathematical project, some code smells are inevitable, which is also part of the motivation for Microsoft developers distributing Z3 as an open source project in GitHub.
Module analysis
With the analysis of code organization, we continue to divide Z3 into the several modules (depicted as folder shape in Figure 7).
- Make and build modules: the preparation for using Z3.
- RiSE4fun module: online tool
- Other projects module: integrat Z3 into other projects.
- Scripts module: supports make and build modules and documents update
- Function modules: core modules containing a series of sub-modules, such as parser, tester, solver, sat and model.
- API, sat and math modules: source code that supports different input formats
- Doc module: generates API and code documents.
- Besides, test module, located in another repository, is a separate part of the whole project, which offers test infrastructure and benchmarks.
Layer and Dependencies
As a software application, three aspects of issues are taken into consideration when developing a software architecture, which are presentation/utility layer, business/domain layer and data/code access layer [7]. This layered structure is used as a reference for our analysis of the Z3 project. We choose to have a support layer rather than data access layer because we think it is more proper.
- Utility layer. This layer is for interaction between users and Z3. We can use Z3 with command line on different platforms. Besides, we can also try Z3 on the website RiSE4fun and insert Z3 into other projects. Make and build modules are important parts of using Z3 with command line. They are used to get preparation before application. These two modules have dependency on the scripts module in the core layer because the python files in the scripts module are necessary to do the make and build executions.
- Core layer. This layer is responsible for the realization of Z3's functions. In the core layer, most modules are for the realization of Z3's functionalities. As a theorem prover, steps necessary to give a correct result of a theorem include parse (to see if syntax and semantics are correct), test (results), solve (the question), judge (if it is a satisfiable(sat) theorem or not), and generate model (if the theorem is a satisfiable one). These modules and their dependencies as shown in Figure 7. Besides, scripts is also a core module of the whole project, without which Z3 cannot be installed and used.
- Support layer. This layer offers basic functions, theories, and formulas to support the operation of the core layer. API, math and smt modules in this layer are all for this purpose. In addition, doc module is also in this layer because it provides API and code documents and is a support of realization and use of Z3.
- Besides, there is a repository called z3test, which holds test infrastructure and benchmarks used to test Z3.
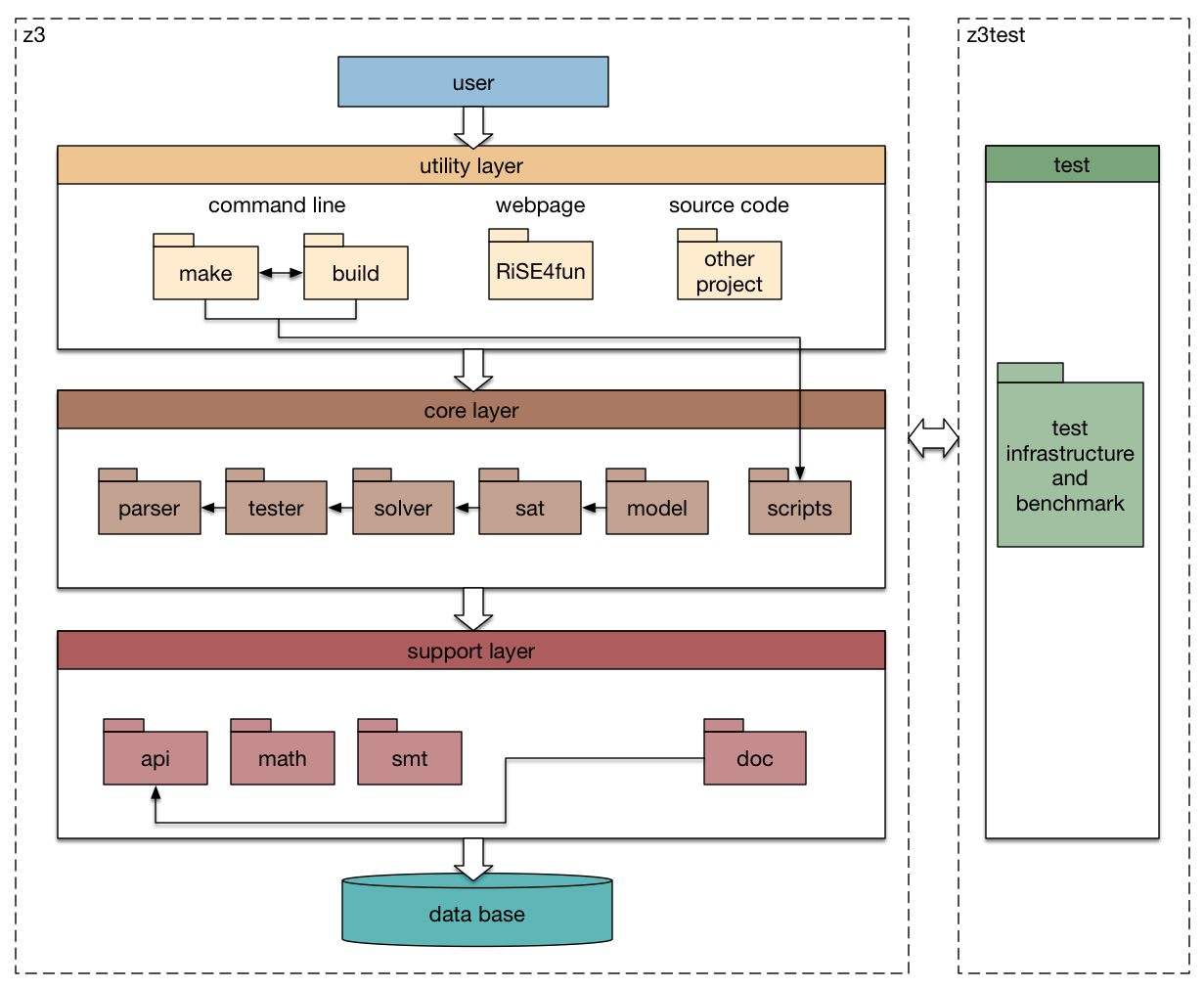
Figure 7. Module structure model [8]
Test Infrastructure
Testing is an important part of software development. As mentioned in the above layer analysis, Z3 has a separate repository z3test to hold its test infrastructure and benchmarks, which include limited tests and benchmarks for both API languages and theory features.
There exists a basic set of regression tests in the directory z3test/regressions. Major theory feature tests such as linear arithmetic, bit-vectors, arrays, and tuples are provided in files prefixed with smt2. New features are continuously added, such as files bounded_quantifier and poirot. Besides, Z3 provides bindings for 6 major API languages (.Net, C, C++, Java, OCaml, and Python). Among all these API languages, however, only C++ and Python tests are currently provided. Developers have been actively encouraging users to contribute to tests and benchmarks for all these 6 languages.
One advance of the test process is that developers provide nightly builds for all major platforms. This infrastructure automatically builds and tests Z3 every night. Previously, they were built using "working-in-progress branch" and if these builds passed the basic set of tests, they would be accepted. The Nightly build is a best practice of continuous integration, which saves excessive computer resources and speeds up the development. This feature is useful for users who find bugs but do not want to wait for the next official release.
Variability Perspective
Feature variability has great influence on a software. The features of a software may affect users decision of choosing the software. Now we focus on feature variability of Z3 to analyze if it has proper features.
Features
According to IEEE 829[9], a feature is defined as a distinguishing characteristic (e.g., performance, portability, or functionality) of a software item. A system is said to be feature-rich when it has many options and functional capabilities available to the user. We list a set of typical features of Z3 in Table 2 [10][11][12][13].
| Feature | Description |
|---|---|
| Compiler | How Z3 can be built |
| API | Programming language used to formulate whatever theories that users want to solve |
| OS | Operating systems that Z3 supports |
| User interface | Where to use Z3 |
| Input formats | How logical formulas will be input |
| Solution generation | After a formula is satisfiable, a user can choose whether to generate a model containing solutions to variables of that formula |
| Theories | Theories that Z3 can solve |
Table 2. Features of Z3
Compiler: Windows users can compile Z3 source code using Visual Studio while other platforms can compile Z3 using a Makefile (based on g++ and clang++) as an alternative.
API: Z3 is a low-level tool. It is best used as a component in the context of other tools that require solving logical formulas. Consequently, Z3 exposes a number of API facilities to make it convenient for tools to map into Z3. These programmatic APIs consist of .NET, C++, C, Java, Ocmal and Python.
OS: Z3 supports all major operating systems including Windows, MacOS X, Linux and FreeBSD, which in turn facilitates the popularity of Z3.
User interface: there is an online tool rise4fun showing main capabilities of Z3 using the textual interface based on SMT 2 language. However, most applications use the Z3 programmatic API to access those features. Those Z3 programmatic APIs can be accessed by building its source code or through an external IDE ACIDE.
Input formats: corresponding to the above user interfaces, logic formulas requiring satisfiability checking and solving can either be input in SMT 2.0 language or in Z3 API (see examples). Besides, native text can also be input into Z3.
Solution generation: users can test if a theory is satisfiable, which is done by the command check-sat when using the online tool rise4fun for example. Moreover, users can choose whether or not to generate a possible solution to that model, which is then done by the command get-model when using rise4fun.
Theories: the essence of Z3 is to check the satisfiability of logical formulas over one or more theories. Users can check satisfiability and get a model for any of the theories that Z3 supports. Therefore, we introduce core theories Z3 supports in detail (try out these features online).
Propositional logic: the pre-defined sort Bool is the sort (type) of all Boolean propositional expressions. Z3 supports the usual Boolean operators
and, or, xor, not, => (implication), ite (if-then-else).Bi-implicationsare represented using equality=.Arithmetic: Z3 has built-in support for integer and real constants, which represent the mathematical integers and reals. The command
declare-constis used to declare integers and real constants.Nonlinear arithmetic: in Z3, a formula is called nonlinear if it contains multiplication in the form (* t s) where t and s are not numbers. Nonlinear real arithmetic is very expensive, and Z3 is not complete for this kind of formula.
Division: Z3 has support for division, integer division, modulo and remainder operators. Internally, they are all mapped to multiplication.
Bit vectors: the theory of bit-vectors allows modeling the precise semantics of unsigned and of signed two-complements arithmetic. Z3 supports bit vectors of arbitrary size. Bit vector literals may be defined using binary, decimal and hexadecimal notation.The command
set-option :pp.bv-literals falsecan be used to force Z3 to display bit vector literals in decimal format.Arrays: as part of formulating a program of a mathematical theory of computation, Z3 contains a decision procedure for the basic theory of arrays. It also contains various extensions for operations on arrays that remain decidable and amenable with an NP-complete satisfiability complexity [14].
Quantifiers: Z3 accepts and can work with formulas that use quantifiers, which outperforms most SMT solvers that support only quantifier-free fragments of their logics.
Relationship
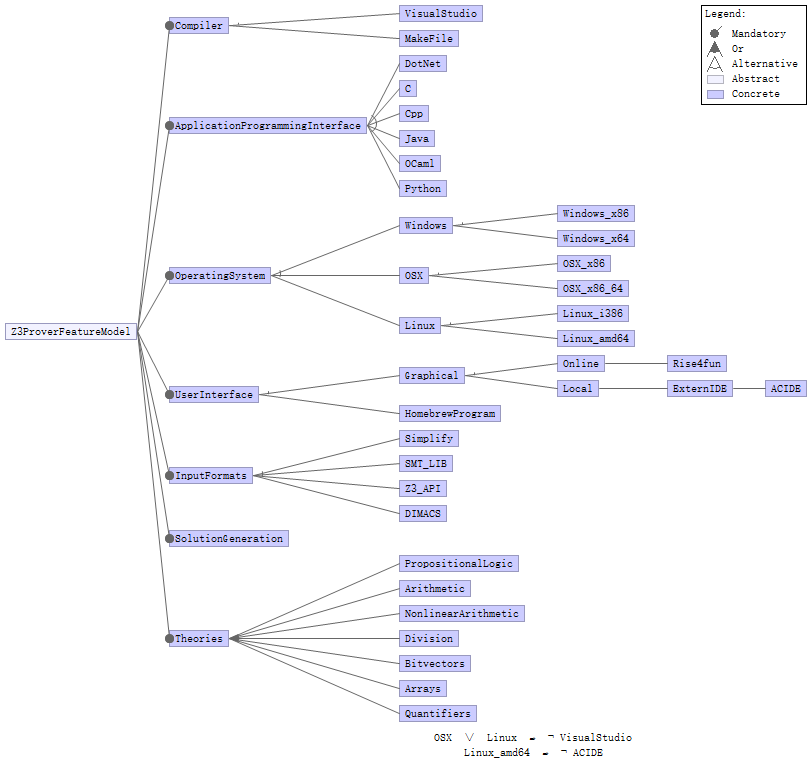
Figure 8. Feature relationship
Starting from a user's perspective, the 1st variation comes with the selection using Z3 online or locally. When using Z3 online there is no variability among the OS being used. However, if Z3 is run locally, the user has to choose whether to use the pre-built binary version, optionally with an external IDE, or invoke the API from a homebrew program. Z3 can be built with Visual Studio or a Makefile. However, Visual Studio is incompatible on Linux or OSX. Additionally, the external IDE did not support x64 version of Windows or Linux originally. Soon after we created the issue for this, they provided support for x64 systems.
Though Z3 itself is mainly coded in C++, it provides multiple APIs in different programming languages in the directory src/api/ for a broader audience. For example, it provides a header file namely z3++.h for C++ users. Also, there is a package namely com.microsoft.z3 for Java users. When using the online version of Z3, the user can only use the parser supported by that website, for example, Z3 at rise4fun only supports SMT-LIB 2.0 standard. When running locally, the user can usually have a broader choice of input formats. Z3 understands a set of default file extensions and calls the right parser in directory src/parsers/ to parse it.
Evolution Perspective
Based on the various features concluded in variability perspective, the evolution of Z3 in the aspect of features is shown in Table 3. Typically, the evolution of a software is recorded with bug fix and new feature introduction. The bug fix part, however, is not involved in the following table. Another point to be aware of is that Z3 has already experienced three years before its settling on GitHub. The evolution analysis after this time point is listed in Table 3 [16].
| Version | New Feature Description |
|---|---|
| 2.0 | (1) The API exposes a new call for check assumption (2) Partial support for non-linear arithmetic (3) Recursive datatypes |
| 2.3 | (1) F# Quotation utilities are supported for expression aspect (2)QUANT_ARITH configuration and complete quantifier-elimination simplification for linear real and linear integer arithmetic |
| 2.4 | (1) Preliminary support for SMT-LIB2 |
| 2.5 | (1) STRONG_CONTEXT_SIMPLIFIER=true allows simplifying sub-formulas to true/false depending on context-dependent information in main theory (2) Some parameter values can be updated over the API and this functionality is called Z3_update_param_value in the C API |
| 2.7 | (1) Added Z3_repeat to create the repetition of bit-vectors (2) Added correction function to_int and testing function is_int to the main theory |
| 2.11 | (1) SMT-LIB 2.0 parsing support for (! ..) in quantifiers and (_ ..) (2) Allow passing strings to function and sort declarations in the .NET theory builders |
| 2.17 | (1) Added command echo [string] to the SMT-LIB 2.0 frontend |
| 2.18 | Z3 has a new mode for solving fixed-point queries |
| 3.0 | (1) Fully compliant SMT-LIB 2.0 (SMT2) front-end (2) Z3 can read dimacs input formulas (3) Performance improvements for linear and nonlinear arithmetic (4) Improved model-based quantifier instantiation |
| 3.2 | (1) Improved OCaml build scripts for Windows. (2) New APIs: Z3 substitute and Z3 substitute_vars |
| 4.0 | (1) New C API (2) New .NET API together with updated version of the legacy (3) Z3Py: Python interface for Z3 (4) NLSAT solver for nonlinear arithmetic (5) The PDR algorithm in muZ |
| 4.1 | (1) New OCAML API (2) CodeContracts in the .NET API |
| 4.3.1 | (1)Added support for compiling Z3 using clang++ on Linux and OSX |
| 4.3.2 | (1) Added preliminary support for the theory of floating point numbers (2) Added get_version() and get_version_string() to Z3Py (3) Added support for FreeBSD (4)Added support for Python 3.x (5) Java bindings |
| 4.4.0 | (1) Support for the theory of floating-point numbers (2) Stochastic local search engine for bit-vector formulas |
Table 3. Evolution of Z3
Deployment view
When choosing a software, in addition to feature variability of the software, users also want to know all the prerequisites. The deployment view of a software describes the environment required for the system to be deployed. The R&W book [8] has introduced a number of environment requirements for a software system. Here we introduce only the most relative ones concerning Z3, namely hardware requirement and third-party software requirement.
Hardware requirement
There is no specific hardware requirement for Z3. Z3 is compatible with most modern computer architectures with different operating systems and no additional hardware is necessary. Also, storage space needed for Z3 is not harsh.
Third-party software requirement
The third-party software requirement deals with prerequisites of Z3 that are not included in the source installation package but need to be installed in advance. These third-party softwares are categorized into the following aspects:
Compiler:
- g++ and clang++ - necessary when building Z3 using the Makefile.
- Visual Studio - necessary when building Z3 on Windows.
Web browser:
- Most web browsers support Z3 Rise4fun online tool.
Text editor:
- No specific text editor is required. Users can choose their favorite text editor to interact with Z3.
External IDE:
- Z3 can be interacted with a specific configurable IDE called ACIDE. Packages for some versions of Windows, Ubuntu and MacOS X are available online.
Programmatic API bindings:
- .NET: to enable building .NET on non-Windows platforms, mono is required.
- Python: python package necessary to be installed in suitable directory prefix.
Documentation generation:
- Doxygen: developers must install doxygens to generate the API documentation at the back end.
- Dot: developers must install dot to generate the code documentation at the back end.
Usability Perspective
In addition to all the above views and perspectives, usability also plays an important part in a software. Usability perspective focuses on aspects that make the use of software more easily and efficiently. The way of using the system should be as easy as possible to all people having interaction with it, such as operations staff, support personnel, maintainers, trainers, and users. Besides, the process flow of the system should be simple, understandable, and consistent.
In this particular case, interaction with humans of a theorem prover should obviously be much easier than the mathematical methods and algorithms behind the screen. The usability perspective also deals with the documents that guide users to formulate and use the non-graphical user interface.
Z3 provides 2 kinds of graphical user interface [1]. One is the web-based interface on RiSE4fun. It mainly contains an input text box and run button. The text box is pre-inputted with an example illustrating the basic arithmetic. Besides, there are links to tutorials for users that are still unfamiliar with the use of RiSE4fun. The other graphical user interface is the external IDE based on ACIDE. This is for the users who want to run Z3 locally in a graphical environment.
The more important interfaces of Z3 are non-graphical user interfaces (APIs). Z3 provides APIs [15] in C, C++, Java, Python, .NET, and OCaml(). By the scripts and doxygen files in the directory doc/, detailed documentations of API and code can be generated, offering users the introduction of the variables of configurations. In the directory examples/, examples of all languages supported and ways to build are provided. These give users an intuition to these APIs and can be used as templates if necessary.
According to all above, Z3 has done a good job with respect to usability.
Conclusion
Applications in artificial intelligence and formal methods for software development have greatly benefited from the recent advances in SAT. Often, however, applications in these fields require determining the satisfiability of formulas in more expressive logics such as first-order logic. Despite the great progress made in the last twenty years, general-purpose first-order theorem provers (such as provers based on the resolution calculus) are typically not able to solve such formulas directly. Faced with this situation, the SMT solver has been invented combining the background theory. Z3, as an outstanding representative in SMT solver, is introduced in this chapter. This software model checking and related algorithmic verification tool holds the potential to close the gap between the programmer’s intent and the actual code. Even though Z3 has already been regarded as a mature tool from the functional perspective, it still has defects in its cross-platform configuration and the way it leads other developers contributing towards it on GitHub. This chapter, therefore, also enclsoses the contribution file to point out the already existed contribution and further potential contribution towards Z3 IDE.
References
- De Moura L, Bjørner N. Generalized, efficient array decision procedures[C]//Formal Methods in Computer-Aided Design, 2009. FMCAD 2009. IEEE, 2009: 45-52.
- Bjørner N, Phan A D. vZ-Maximal Satisfaction with Z3[C]//SCSS. 2014: 1-9.
- Blog by Georgios Gousios, http://www.gousios.gr/blog/How-do-project-owners-use-pull-requests-on-Github/.
- De Moura L, Bjørner N. Z3: An efficient SMT solver[M]//Tools and Algorithms for the Construction and Analysis of Systems. Springer Berlin Heidelberg, 2008: 337-340.
- Blog of @leodemoura, http://leodemoura.github.io/blog.html.
- Three-Layered Services Application, https://msdn.microsoft.com/en-us/library/ff648105.aspx.
- Rozanski N, Woods E. Software systems architecture: working with stakeholders using viewpoints and perspectives[M]. Addison-Wesley, 2012.
- IEEE Standard for Software and System Test Documentation[S]//IEEE Std 829-2008. 2008: 1-150.
- Z3 SMT 2.0 online tutorial, http://rise4fun.com/z3/tutorial/guide.
- Z3 Sequences tutorial, http://rise4fun.com/Z3/tutorial/sequences.
- Z3 Fixed-point tutorial, http://rise4fun.com/Z3/tutorial/fixedpoints.
- Z3 Strategies tutorial, http://rise4fun.com/Z3/tutorial/strategies.
- De Moura L, Bjørner N. Generalized, efficient array decision procedures[C]//Formal Methods in Computer-Aided Design, 2009. FMCAD 2009. IEEE, 2009: 45-52.
- Z3 API documentation, http://z3prover.github.io/api/html/index.html
- Z3 solver RELEASE_NOTES, https://github.com/Z3Prover/z3/blob/master/RELEASE_NOTES.